ディープラーニングの勉強がてらに歴史を振り返ろうと思ったので、今回はCNNの元祖となるLeNetの論文(http://yann.lecun.com/exdb/publis/pdf/lecun-89.pdf)を読んてみました。
この論文を読むまで知らなかったのですが、私達がよくLeNetと呼ぶのは1998年に発表されたLeNet-5のことでオリジナルのLeNetとは違うんですね。今回は1989年に発表されたLeNetを実装してみます。
LeNetとは
LeNetは以下の画像のような2層の畳み込み層と1層の全結合層からできているネットワークです。
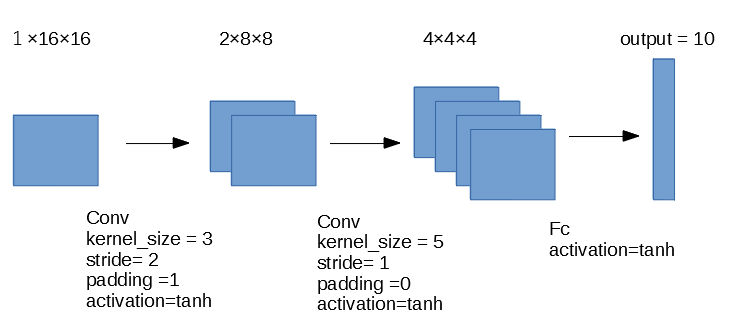
個人的に最近のCNNと比べて大きく違うところは、Pooling層がないところだと思っています。
また活性化関数はtanhが使われているようで、この時はReLUがまだ存在しないというのが時代を感じさせられます。
ただこの論文では現在のCNNでも使われているWeight Sharing(重み共有)の考えがあったようで、パラメータを減らすための工夫がなされているのが感動的です。
学習データについて
LeNetは以下のような手書きの数字を学習データとして使用しています。

画像のサイズは16×16とMNISTと比べても少し小さな画像となっています。
また、訓練データが320枚、テストデータが160枚の計480枚と学習データはかなり小さいです。
現代と違い手書き数字ですらデータセットが整っていなかったようですね。
LeNetの実装
それではLeNetを実装してみます。
本来であれば論文通りに実装するのが良いのかもしれませんが、現代のDNNとは少し構造も違うことがあり、実装が大変だったため今回はLeNetライクな実装をしてみました。
# -*- coding: utf-8 -*-
from torch import nn
import torch.nn.functional as F
class LeNet(nn.Module):
def __init__(self) -> None:
super(LeNet, self).__init__()
self.conv1 = nn.Conv2d(
in_channels=1, out_channels=2, kernel_size=3,
stride=2, padding=1)
self.conv2 = nn.Conv2d(
in_channels=2, out_channels=4, kernel_size=5,
stride=1, padding=0
)
self.fc = nn.Linear(4*4*4, 10)
def forward(self, x):
x = F.tanh(self.conv1(x))
x = F.tanh(self.conv2(x))
x = F.tanh(self.fc(x.view(-1, 4*4*4)))
return xこうやって実装してみるとやはり現代のモデルと比べても層が少なくシンプルな実装であることが分かります。
MNISTを学習させてみた
LeNetと訓練データを合わせるのか少し悩んだのですが、せっかく大規模なデータができた現代での実装ということでMNISTで学習させてみました。
学習コードは以下のとおりです。
import torch
import torchvision
import torchvision.transforms as transforms
from torch import nn, optim
from LeNet5 import LeNet5
preprocess = transforms.Compose([
transforms.Resize(16),
transforms.ToTensor(),
])
trainset = torchvision.datasets.MNIST(
root='./data',
train=True,
download=True,
transform=preprocess
)
testset = torchvision.datasets.MNIST(
root='./data',
train=False,
download=True,
transform=preprocess
)
batch_size = 100
trainloader = torch.utils.data.DataLoader(
trainset,
batch_size=batch_size,
shuffle=True,
)
testloader = torch.utils.data.DataLoader(
testset,
batch_size=batch_size,
shuffle=False,
)
# 使用するデバイスの設定
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(device)
# 損失関数とオプティマイザの定義
net = LeNet5()
net = net.to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.01)
# ネットワークの訓練
epochs = 100
net.train()
for epoch in range(epochs):
loss = None
count = 0
train_acc = 0
for i, data in enumerate(trainloader, 0):
inputs, labels = data[0].to(device), data[1].to(device)
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 訓練データの精度を計算
pred = outputs.argmax(dim=1, keepdim=True)
train_acc += pred.eq(labels.view_as(pred)).sum().item()
count += inputs.shape[0]
train_acc = (train_acc/count) * 100
print("epoch{:d}/{:d} train_loss:{:.3f} train_acc:{:.2f}".format(epoch+1, epochs, loss, train_acc))
# モデルを保存
torch.save(net.state_dict(), './LeNet_mnist.pth')
# testデータで評価
test_acc = 0
count = 0
net.eval()
with torch.no_grad():
for data in testloader:
inputs, labels = data[0].to(device), data[1].to(device)
outputs = net(inputs)
pred = outputs.argmax(dim=1, keepdim=True)
test_acc += pred.eq(labels.view_as(pred)).sum().item()
count += inputs.shape[0]
acc = (test_acc / count) * 100
print(acc)100epoch学習させてみたところテストデータに対する制度は92.32%となかなかの結果です。
MNISTぐらいのシンプルなデータであればLeNetでも十分なのかもしれません。
逆に最新のモデルなんかを実務で郵便番号の判別などに使用してみると、モデルが大きいことで処理速度が微妙になる可能性もあるのでシンプルなモデルと使い分けるのも大切かもしれませんね。
参考
LeCun, Yann. “Generalization and network design strategies.” Connectionism in perspective 19 (1989): 143-155.

コメント