ディープラーニングの目的は損失関数の値をできるだけ小さくするパラメータを見つけることです。
そのパラメータを見つけることを最適化(optimization)と呼び、最適化を行うための手法のことを最適化アルゴリズム(optimizer)という。
様々な最適化アルゴリズム
SGD(確率的勾配降下法)
SGDは勾配方向にパラメータを少しずつ近づけていき、最適なパラメータを見つける手法です。
$$W=W-\eta\frac{dL}{dW}$$
勾配降下法のアルゴリズムなどは詳しくは以下の記事に書いていますので合わせて確認してください。
SDGの欠点は関数によっては勾配の方向が最小ではない方向を指していることがあるため、最適な値にたどり着くまでに非効率な経路を通るところです。
例えば以下の関数の最小値をSGDを使って探してみます。
$$f(x, y)=\frac{1}{20}x^2+y^2$$
グラフを見ると経路がジグザグしており、非効率なことが分かります。
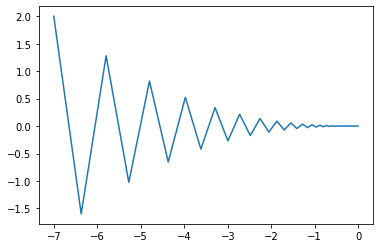
Momentum
MomentumはSGDに運動量(モーメンタム)という考え方を導入した手法です。
Momentumは前回の更新までの転がり具合を保ったまま、逆向きの傾斜に更新するためSGDとくらべてパラメータがなめらかに更新されていきます。
更新式は次のようになっています。
$$v=\alpha v-\eta\frac{dL}{dW}$$
$$W=W+v$$
\(f(x, y)=\frac{1}{20}x^2+y^2\)の最小値をMomentumを使用して探索すると、SGDを使用したときと比べてなめらかに更新されていることが分かります。
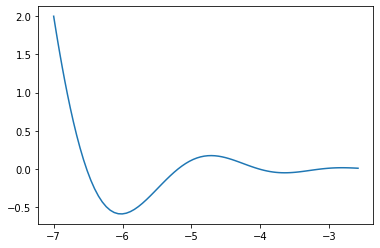
AdaGrad
AdaGradは学習が進んでいるパラメータの学習率を小さくして、学習が進んでいないパラメータの学習率を大きくするという手法です。
パラメータの要素ごとに適応力を見ながら学習率を調整するため効率よく学習を進めることができます。
更新式は次のようになっています。
$$h=h+\frac{dL}{dW}\bigodot\frac{dL}{dW}$$
$$W = W-\eta\frac{1}{\sqrt{h}}\frac{dL}{dW}$$
\(f(x, y)=\frac{1}{20}x^2+y^2\)の最小値をAdaGradを使用して探索してみると効率よく最小値の方向に向かっていることが分かります。
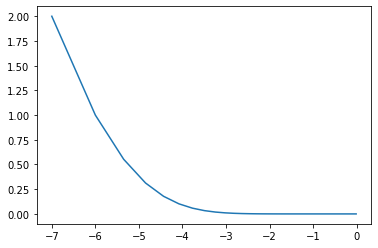
欠点として無限に学習を進めると学習率を調整している\(h\)の値が0になり、更新量が0になってしまい学習を続けることができなくなるという問題点があります。
この問題を改善した手法としてRMSPropがありますが本記事では解説は割愛します。
Adam
AdamはMomentumとAdaGradの良いところを取った手法です。
別記事でAdamについての解説は書かせていただきます。
まとめ
今回は3つの最適化アルゴリズムを紹介しました。
どの手法が有効化は解く問題によって異なってくるため、ハイパーパラメータと同様に最適化アルゴリズムも検討することが大切です。

コメント