誤差逆伝播法とは
誤差逆伝播法(back propagation)とは関数の偏微分を効率的に計算する方法のことです。
数値微分は実装は簡単だが、計算に膨大な時間がかかるという問題がありそれを解決したのが誤差逆伝播法になります。
誤差逆伝播法の解説方法として数式を使ったものと計算グラフを使用したものがあるのですが、本記事ではゼロつくに則って計算グラフを使用して解説していきます。
計算グラフとは
計算グラフの概要
100円のリンゴを2個買い、消費税が10%のときの合計金額を求めたい場合、計算グラフでは次のように表現することができます。
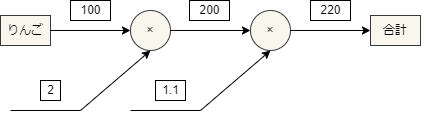
このように計算を左から右に順に進めることを順伝搬という。
ここでリンゴの値段が値上がりした場合に支払金額にどうのような影響が出るのか知りたいとします。
これはリンゴの値段に関する支払金額の微分を求めることに相当します。このような微分は計算グラフを逆方向に伝搬することで求めることができます。
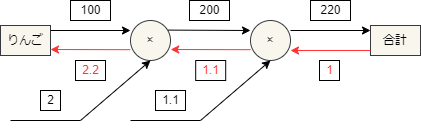
上の例からはリンゴが1円値上がりすると、合計が2.2円増えるということがわかります。
このように順伝搬と逆の方向で計算していくことを逆伝播といいます。
先程の例を少し数学的に落とし込んでみます。
例えば\(y=f(x)\)という関数の逆伝播を計算グラフで書くと以下のようになります。
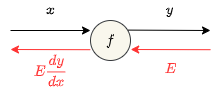
計算グラフを使うことで逆伝播を直感的に理解することができるというメリットがあります。
連鎖律
連鎖率とは合成関数の微分についての性質で、ある関数が合成関数で表される場合、その合成関数の微分は、合成関数を構成するそれぞれの関数の微分の積によって表すことができるというものです。
つまり合成関数の微分は計算グラフ上で、前回の経路の微分の値との積で表すことができるということです。
以下のような合成関数があるとします。
$$z=t^2$$
$$t=x+y$$
この関数の微分を計算グラフで表現すると以下のようになり、合成関数の微分がそれぞれの関数の微分の積で表すことができていることが分かります。
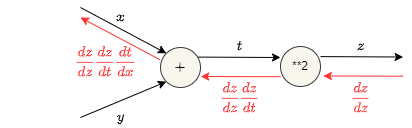
様々なレイヤの逆伝播
計算グラフの仕組みが分かったところで深層学習で使用するいくつかのレイヤの逆伝播を計算グラフを使用して表現していきます。
加算レイヤ
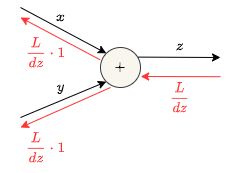
加算レイヤが\(z=x+y\)のような式だとします。
\(x\)に関する\(z\)の微分は\(\frac{dz}{dx}=1\)、\(y\)に関する\(z\)の微分は\(\frac{dz}{dy}=1\)のように表現することができます。
これを計算グラフで書くと次の通りになります。
乗算レイヤ
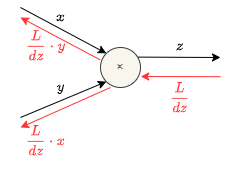
乗算レイヤが\(z=xy\)のような式だとします。
\(x\)に関する\(z\)の微分は\(\frac{dz}{dx}=y\)、\(y\)に関する\(z\)の微分は\(\frac{dz}{dy}=x\)のように表現することができます。
これを計算グラフで書くと次の通りになります。
ReLUレイヤ
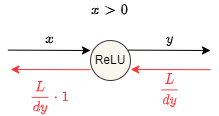
ReLUレイヤは\(y=\begin{cases}{x (x>0)}\\{0(x\leq0)}\end{cases}\)という関数です。
ReLUレイヤの微分は\(\frac{dy}{dx}=\begin{cases}{1 (x>0)}\\{0(x\leq0)}\end{cases}\)であり、これを計算グラフで表すと次のようになります。
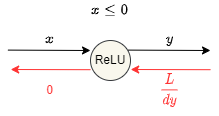
このように計算グラフを使用することで深層学習で用いる様々なレイヤの逆伝播を直感的に理解することができ、自分で新たなレイヤを作成したいときなどに役立ちます。

コメント