【ゼロつく学習記録】『損失関数』を理解する

損失関数(Loss Function)とは

損失関数はニューラルネットワークの性能の悪さを示す指標である。

ニューラルネットワークでは最適なパラメータを求めるために使用する。

$$E = \frac{1}{2}\sum_{k}(y_k – t_k)^2$$

２乗和誤差各は各データに対して正解値と予測値の差の２乗を計算しその総和をデータ数で割った値を出力する関数である。

誤差を２乗することから誤差が大きいほど過大に評価するため、間違いを重要視するという特徴がある。

$$E = -\sum_{k}t_k\log y_k$$

分類問題の場合、t_kは正解ラベル以外は0になるため、交差エントロピー誤差の値は正解ラベルの自然対数の和になる。

自然対数は以下のグラフで表すことができる。

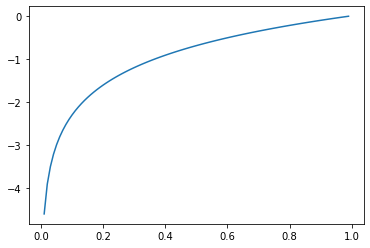
このグラフから交差エントロピー誤差が0に近いほど誤差が少ないことが分かる。

ニューラルネットワークで学習を行う際に全てのデータに対して損失関数を求めることができるが、その場合計算に多大な時間がかかるという問題が発生する。

そこでランダムにN個のデータを選択し、損失関数を計算することで近似値を求める方法をニューラルネットワークでは使用する。

ランダムにデータを選ぶことをミニバッチと呼び、ミニバッチごとに損失関数を求め学習を行うことをミニバッチ学習と呼ぶ。

認識精度が高くなるように重みやバイアスのパラメータを設定するのに、認識精度ではなく損失関数を指標とする理由は認識精度を微分するとほとんどの場合に0になるからだ。

微分が0になるとパラメータを更新することができなくなってしまう。これを防ぐために損失関数を使用する。

認識精度の微分の値が殆どの場合に0になる理由は、認識精度は損失関数の値のように連続値をとることができない(32%, 33%のようにとびとびの値である)からだ。

そのためパラメータの微小な変化では認識精度ほとんど変化がない。

それに比べ損失関数は微小なパラメータの変化に対しても値が連続的に変化する。

以上のことがパラメータの更新に認識精度ではなく損失関数を設定する理由だ。