勾配とは
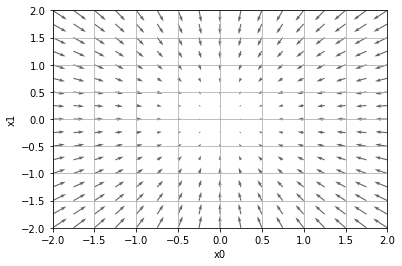
以下のような式があるとき\((x_0, x_1)\)のように全ての変数に対するの偏微分を求めて\((\frac{df}{dx_0}, \frac{df}{dx_1})\)のようにベクトル化したものを勾配と呼ぶ。
$$f(x_0, x_1)=x_0^2+x_1^2$$
勾配は各地点において関数の値を最も減らす方向を指している。
勾配降下法
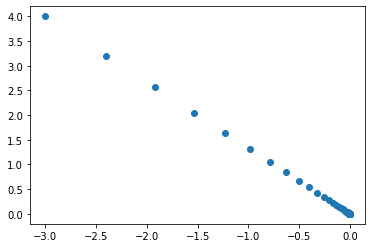
ある地点での勾配を求めて、少しずつパラメータを勾配の方向にずらすことで最小値を探す方法のことを勾配降下法という。
例えば先程の\(x_0, x_1)\という関数の場合、パラメータの更新は以下の式で表すことができる。
$$x_0 = x_0 – \eta\frac{df}{dx_0}$$
$$x_1 = x_1 – \eta\frac{df}{dx_1}$$
\(\eta\)は1回の学習でどれだけ値を更新するかを決めるパラメータで学習率と呼ばれる。
学習率はハイパーパラメータの一種である。学習率が大きすぎたり小さすぎたりする場合良い場所にたどり着くことができないので、適切な値を決めることが重要である。
\(x_0^2+x_1^2\)は勾配降下法によるパラメータの更新を繰り返すことで\(x_0=0, x_1=0\)に近づく。
ニューラルネットワークに対する勾配
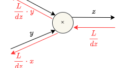
ニューラルネットワークにおける学習の勾配とは重みパラメータに関する損失関数の勾配である。
損失関数を\(L\)としたときに以下のような重み\(Wを持つニューラルネットワークがあるとする。
$$W = \begin{pmatrix}w_{11} & w_{12} & w_{13}\end{pmatrix}$$
それぞれの要素の偏微分を求めると以下のようになる。
$$\frac{dL}{dW} = \begin{pmatrix}\frac{dL}{w_{11}} & \frac{dL}{w_{12}} & \frac{dL}{w_{13}}\end{pmatrix}$$
これは\(w_{11}\)を\(h\)増やすと損失関数の値は\(\frac{dL}{w_{11}}h\)増えるということを意味する。
また、ニューラルネットワークはミニバッチで選択した値に対して損失関数を求める。
このようにミニバッチで選んだデータで勾配降下法を行うことを確率的勾配降下法(stochastic gradient descent, SGD)という。

コメント